Rolle's Theorem

Rolle's Theorem is similar to a well known adage--even though it looks inscrutable at first glance.

Theorem: If f(x) is
1). continuous on [a,b] and
2). f(x) is differentiable on (a,b) and
3). f(a)=f(b), then
there is some number c in (a,b) such that f'(c)=0.

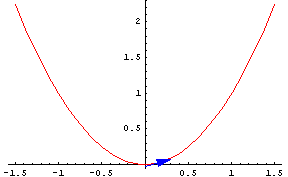
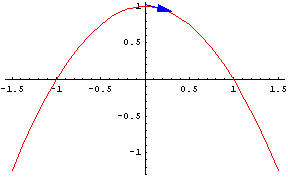
The functions in the following graphs match the three conditions. Click on the graphs and answer the questions.

The first example shows the tangent lines switch from pointing up to pointing down. You have seen a demonstration of the adage, "What goes up, must come down." The second shows the reverse, the tangent lines switch from pointing down to pointing up. What went down, came back up.

If something switches from pointing up to pointing down or vice versa, somewhere in between it must be level. This is Rolle's Theorem. For a continuous function, if it starts and ends at the same height then somewhere in between there is a horizontal tangent line.