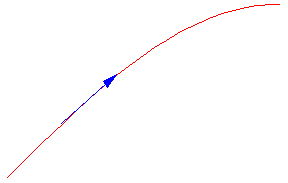

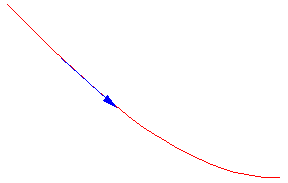
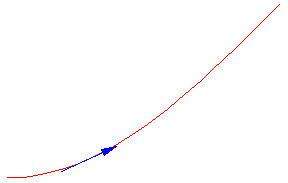
In addition to studying the limits of functions and determining their increasing and decreasing segments, we can study the concavity of functions. Think about a contact lens. If it is sitting with the round side against a table, we would say that it is concave. In calculus we call this "concave up." However, if it is sitting with the flat side down on a glass table and we look at if from underneath it still appears to be concave. In calculus we call this "concave down." In case you were wondering, "convexity" has an unrelated meaning in mathematics, so we don't use that word to describe concavity.
Watch each of the following four animations and answer the questions.
 |
 |
 |
 |
Question four is about the concavity. You determined whether the steepeness was increasing or decreasing. This is the rate of change (derivative) of the slope which is the first derivative. Thus concavity is determined by the second derivative.
A function f(x) is
A function f(x) is
Notice that this definition matches our example of the contact lens used above.