
Lists with Distinct Elements
A Geometric Approach
Often we want to count the number of ways to fill a few positions. For example, consider the number of ways of filling the President and Vice-President positions in the Clemson Linux Club. Suppose that the club has 19 members, all of whom are eligible for both positions. We assume that one person is not allowed to fill both positions. Linux is about openness not dictatorship!
The easiest way to count the number of possibilities is to recognize that there are 19 ways to fill the President position. After the President has been chosen, there are only 18 remaining, eligible members. Thus the total number of possible choices for officers is 19*18.
A second way to count the possibilities is slightly more geometric. Create a table with each member listed in alphabetic order down the rows and across the columns. In each cell of the table enter the name for that row then the name for the column. Each entry represents a possible way of filling both positions from the 19 people. There are clearly 19*19 total possibilities. However, we have counted some non-allowed possibilities. The entries on the diagonal have the same person in both positions. There are 19 different ways to pick the same person for both offices. Thus the correct count of the possibilities is 19^2-19=19(19-1)=19*18.
Later the group decides to become an official Clemson University student organization. They are now required to add a third position which they title Web Master. How many ways are there to fill the three positions?
Counting the easiest way we note that there are 19 people who can fill the President position. After the President has been chosen, there are 18 people who can fill the Vice-President position. After both those positions have been chosen, there are only 17 people left to pick the Web Master from. Thus the total number of possibilities is 19*18*17.
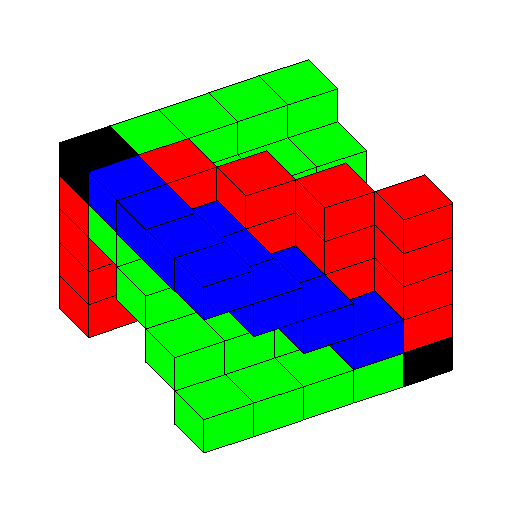
It is possible to use the geometric presentation as well. This time instead of writing down a table (a square), we write the entries in a cube. To construct the cube consider laying 19 square blocks in a row. Add 19 square blocks next to the first row. Add a third, fourth, through a nineteenth row of blocks. This has created one layer (square) of blocks. Now create a new layer on top of the first layer. Create a total of 19 layers. There are now 19^3 blocks forming a larger cube. Each block represents a different possibility. The row represents the president, the column represents the vice-president, and the height represents the web master.
19^3 over counts the number of possibilities, because it includes one person serving in multiple offices. We enumerate now these over counts. It is possible that the same person was picked for president and vice-president represent this as (a,a,b). The same person may have been picked for president and web master, which we represent by (a,b,a). The same person may have been picked for vice-president and web master, which we represent by (b,a,a).
These disallowed options form diagonal planes in our cube. To visualize this consider the first layer of blocks that you layed. Each element of the diagonal with same x and y coordinate represented electing the same person as president and vice-president. On the second layer you layed another diagonal with the same president and vice-president but with a different web master from the first layer. As you added the layer you built up a diagonal plane of choices with the same president and vice-president. These are represented on the examples below as the red blocks.
The same reasoning can be used for the other two possibilities (a,b,a) and (b,a,a). These are represented by the green and blue blocks in the examples below.
Note that we did not assuming that a and b are different, that is one person may have been picked for all three offices. This would be represented by (a,a,a). There are of course 19 ways to do this. In the enumeration (a,a,b), (a,b,a), and (b,a,a) we counted these 19 possibilities three times (once in each representation). These possibilities with one person in all three offices represented by are black cubes down a diagonal from the origin (bottom left corner) to the opposite corner (upper right). That they are counted once in each of the previous cases implies that this diagonal is a line in all three planes.
Finally to get our count we want all the blocks that are not red, green, blue, or black. We obtain 19^3-3*19^2+2*19, which does indeed rearrange to be 19*18*17.

