What is a Graph?

Section 1.2 What is a Graph?

Problem 1.2.3.

Based on the examples in Figure 1.2.1 and Figure 1.2.2 determine which of the following are graphs.

Solution.

These three figures represent a graph. They contain no repeated vertices, or dots. Nor do these figures have any discontinuities. In other words, they have some sort of starting and end points. That being said they also have a finite set of vertices.

\begin{equation*} \left( \begin{array}{*{5}{c}} 0 \amp 1 \amp 1 \amp 1 \amp 1 \\ 1 \amp 0 \amp 0 \amp 0 \amp 0 \\ 1 \amp 0 \amp 0 \amp 0 \amp 0 \\ 1 \amp 0 \amp 0 \amp 0 \amp 1 \\ 1 \amp 0 \amp 0 \amp 1 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{2}{c}} 0 \amp 0 \\ 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{3}{c}} 0 \amp 1 \amp 1 \\ 1 \amp 0 \amp 1 \\ 1 \amp 1 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{2}{c}} \begin{array}{*{3}{c}} 0 \amp 1 \amp 1 \\ 1 \amp 0 \amp 1 \\ 1 \amp 1 \amp 0 \end{array} \amp \\ \amp \begin{array}{*{3}{c}} 0 \amp 1 \amp 1 \\ 1 \amp 0 \amp 1 \\ 1 \amp 1 \amp 0 \end{array} \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{5}{c}} 0 \amp 1 \amp 0 \amp 1 \amp 0 \\ 1 \amp 0 \amp 1 \amp 1 \amp 0 \\ 0 \amp 1 \amp 0 \amp 0 \amp 1 \\ 1 \amp 1 \amp 0 \amp 0 \amp 0 \\ 0 \amp 0 \amp 1 \amp 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{1}{c}} 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{4}{c}} 0 \amp 0 \amp 1 \amp 0 \\ 0 \amp 0 \amp 1 \amp 0 \\ 1 \amp 1 \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{6}{c}} 0 \amp 1 \amp 1 \amp 0 \amp 0 \amp 0 \\ 1 \amp 0 \amp 1 \amp 0 \amp 0 \amp 0 \\ 1 \amp 1 \amp 0 \amp 0 \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \amp 0 \amp 1 \amp 1 \\ 0 \amp 0 \amp 0 \amp 1 \amp 0 \amp 1 \\ 0 \amp 0 \amp 0 \amp 1 \amp 1 \amp 0 \end{array} \right) \end{equation*}

Figure 1.2.4. Each of these is a graph

\begin{equation*} \left( \begin{array}{*{4}{c}} 0 \amp 2 \amp 0 \amp 0 \\ 2 \amp 0 \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \amp 2 \\ 0 \amp 0 \amp 2 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{2}{c}} 0 \amp 0 \\ 0 \amp 1 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{4}{c}} 0 \amp 1 \amp 1 \amp 0 \\ 1 \amp 0 \amp 1 \amp 1 \\ 0 \amp 1 \amp 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{3}{c}} 0 \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{3}{c}} 0 \amp 0 \amp 1 \\ 1 \amp 0 \amp 1 \\ 0 \amp 1 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{3}{c}} 0 \amp 1 \amp 1 \\ 1 \amp 1 \amp 0 \\ 1 \amp 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{4}{c}} 0 \amp 0 \amp 1 \amp 2 \\ 0 \amp 0 \amp 1 \amp 1 \\ 1 \amp 1 \amp 0 \amp 0 \\ 2 \amp 1 \amp 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{4}{c}} 0 \amp 1 \amp 0 \amp 1 \\ 1 \amp 0 \amp 1 \amp 1 \\ 0 \amp 1 \amp 1 \amp 1 \\ 1 \amp 0 \amp 1 \amp 0 \end{array} \right) \end{equation*}

Figure 1.2.5. Each of these is not a graph

Problem 1.2.6.

Based on the examples in Figure 1.2.4 and Figure 1.2.5 determine which of the following are graphs.

\begin{equation*} \left( \begin{array}{*{4}{c}} 0 \amp 1 \amp 2 \amp 0 \\ 1 \amp 0 \amp 0 \amp 0 \\ 2 \amp 0 \amp 0 \amp 0 \\ 0 \amp 0 \amp 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{3}{c}} 0 \amp 1 \amp 0 \\ 0 \amp 0 \amp 1 \\ 1 \amp 1 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{3}{c}} 0 \amp 0 \amp 1 \\ 0 \amp 0 \amp 0 \\ 1 \amp 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{5}{c}} 0 \amp 1 \amp 1 \amp 0 \amp 0 \\ 1 \amp 0 \amp 1 \amp 0 \amp 0 \\ 1 \amp 1 \amp 0 \amp 1 \amp 1 \\ 0 \amp 0 \amp 1 \amp 0 \amp 0 \\ 0 \amp 0 \amp 1 \amp 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{2}{c}} 0 \amp 1 \\ 1 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{2}{c}} 1 \amp 0 \\ 0 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{4}{c}} 0 \amp 1 \amp 0 \amp 1 \\ 1 \amp 0 \amp 1 \amp 0 \\ 0 \amp 1 \amp 0 \amp 1 \\ 1 \amp 0 \amp 1 \amp 0 \end{array} \right) \end{equation*}

\begin{equation*} \left( \begin{array}{*{4}{c}} 0 \amp 1 \amp 1 \amp 1 \\ 0 \amp 0 \amp 1 \amp 1 \\ 0 \amp 0 \amp 0 \amp 1 \\ 0 \amp 0 \amp 0 \amp 0 \end{array} \right) \end{equation*}

Solution.

Which of the following matrices are graphs?

Matrix A is not a graph, since there exists vertexes which are joined by two or more edges.
Matrix B is not a graph, since the second vertex is connected by an edge to the first vertex accoring to one row but the edge doesn't exist in the columns.
Matrix C is a graph since it is symmetric around the centre diagonal line, there are no entries with a "2", and the main diagonal is comprimsed only of zeros.
Matrix D is a graph since it is symmetric around the centre diagonal line, there are no entries with a "2", and the main diagonal is comprimsed only of zeros.
Matrix E is a graph since it is symmetric around the centre diagonal line, there are no entries with a "2", and the main diagonal is comprimsed only of zeros.
Matrix F is not a graph since it shows the first vertex being connected to itself by a single edge.
Matrix G is a graph since it is symmetric around the centre diagonal line, there are no entries with a "2", and the main diagonal is comprimsed only of zeros.
Matrix H is not a graph since it is not symmetric around the main diagonal.

\begin{align*} P = \amp \{p_1,p_2,p_3\}\\ Q= \amp \{q_1,q_2,q_3\}\\ q_1 \leftrightarrow \amp p_1,p_2\\ q_2 \leftrightarrow \amp p_1,p_3\\ q_3 \leftrightarrow \amp p_2,p_3 \end{align*}

\begin{align*} P= \amp \{p_1,p_2,p_3,p_4\}\\ Q = \amp \emptyset \end{align*}

\begin{align*} P= \amp \{p_1,p_2,p_3,p_4\}\\ Q= \amp \{q_1,q_2\}\\ q_1 \leftrightarrow \amp p_1,p_3\\ q_2 \leftrightarrow \amp p_2,p_4 \end{align*}

\begin{align*} P= \amp \{p_1,p_2,p_3,p_4,p_5\}\\ L= \amp \{\ell_1,\ell_2,\ell_3,\ell_4,\ell_5,\ell_6\}\\ \ell_1 \leftrightarrow \amp p_2,p_3\\ \ell_2 \leftrightarrow \amp p_1,p_4\\ \ell_3 \leftrightarrow \amp p_4,p_5\\ \ell_4 \leftrightarrow \amp p_1,p_5\\ \ell_5 \leftrightarrow \amp p_2,p_4\\ \ell_6 \leftrightarrow \amp p_2,p_5 \end{align*}

\begin{align*} V= \amp \{c,d,e,f\}\\ E= \amp \{cd,de,ef,cf\} \end{align*}

\begin{align*} V= \amp \{v_1,v_2,v_3,v_4\}\\ E= \amp \{v_1v_2,v_1v_3,v_2v_3,v_2v_4\} \end{align*}

\begin{align*} P= \amp \{p\}\\ Q= \amp \emptyset \end{align*}

\begin{align*} P= \amp \{q,r,s,t\}\\ Q= \amp \{qr,rt,qt,rs\} \end{align*}

Figure 1.2.7. Each of these is a graph

\begin{align*} P= \amp \{p_1,p_2,p_3\}\\ Q= \amp \{q_1,q_2\}\\ q_1 \leftrightarrow \amp p_1,p_2\\ q_2 \leftrightarrow \amp p_3,p_4 \end{align*}

\begin{align*} P= \amp \{p_1,p_2\}\\ Q= \amp \{q_1,q_2\}\\ q_1 \leftrightarrow \amp p_1,p_2\\ q_2 \leftrightarrow \amp p_1,p_2 \end{align*}

\begin{align*} P= \amp \{p_1,p_2,p_3\}\\ Q= \amp \{q_1,q_2,q_3\}\\ q_1 \leftrightarrow \amp (p_1,p_2)\\ q_2 \leftrightarrow \amp (p_1,p_3)\\ q_3 \leftrightarrow \amp (p_2,p_3) \end{align*}

\begin{align*} V= \amp \{x,y,z\}\\ E= \amp \{f,g,h\}\\ f \leftrightarrow \amp x,y\\ g \leftrightarrow \amp y,x\\ h \leftrightarrow \amp y,z \end{align*}

\begin{gather*} P=\emptyset\\ Q=\emptyset \end{gather*}

\begin{align*} P= \amp \{q,r,s,t\}\\ Q= \amp \{qr,rt,ss\} \end{align*}

\begin{align*} V= \amp \{p_1,p_2,\ldots,p_n,\ldots\}\\ E= \amp \{p_1p_2,p_2p_4,p_1p_3,p_4p_6\} \end{align*}

\begin{align*} P= \amp \{p_1,p_2,p_3\}\\ Q= \amp \{q_1,q_2,q_3\}\\ q_1 \leftrightarrow \amp p_1,p_2\\ q_2 \leftrightarrow \amp p_1,p_3 \end{align*}

Figure 1.2.8. Each of these is not a graph

Problem 1.2.9.

Based on the examples in Figure 1.2.7 and Figure 1.2.8 determine which of the following are graphs.

\begin{gather*} P=\{p_1,p_2,p_3\}\\ Q=\{q_1\}\\ q_1 \leftrightarrow p_1,p_3 \end{gather*}

\begin{gather*} P=\{p_1,p_2,p_3\}\\ Q=\{q_1,q_2\}\\ q_1 \leftrightarrow p_1,p_2 \end{gather*}

\begin{gather*} V=\{v_1,v_2,\ldots,v_n,\ldots\}\\ E=\{e_1,e_2,\ldots,e_n,\ldots\}\\ e_1 \leftrightarrow v_1,v_2\\ \vdots\\ e_n \leftrightarrow v_n,v_{n+1}\\ \vdots \end{gather*}

\begin{gather*} P=\{p,q,r\}\\ Q=\{t,u,v\}\\ t \leftrightarrow p,q\\ u \leftrightarrow p,r\\ v \leftrightarrow q,r \end{gather*}

\begin{gather*} P=\{p_1,p_2,p_3\}\\ Q=\emptyset \end{gather*}

\begin{gather*} V=\{u_1,u_2,u_3,u_4\}\\ E=\{u_1u_2,u_2u_1,u_3u_4\} \end{gather*}

\begin{gather*} V=\{v_1,v_2,v_3\}\\ E=\{v_1v_2,v_1v_3,v_3v_3\} \end{gather*}

\begin{gather*} P=\{p,q,r,s\}\\ Q=\{pq,pr,ps,qr,qs,rs\} \end{gather*}

Solution.

1: Is a graph. Each vertex and edge in the graph is defined. This graph is finite and has no repititions.
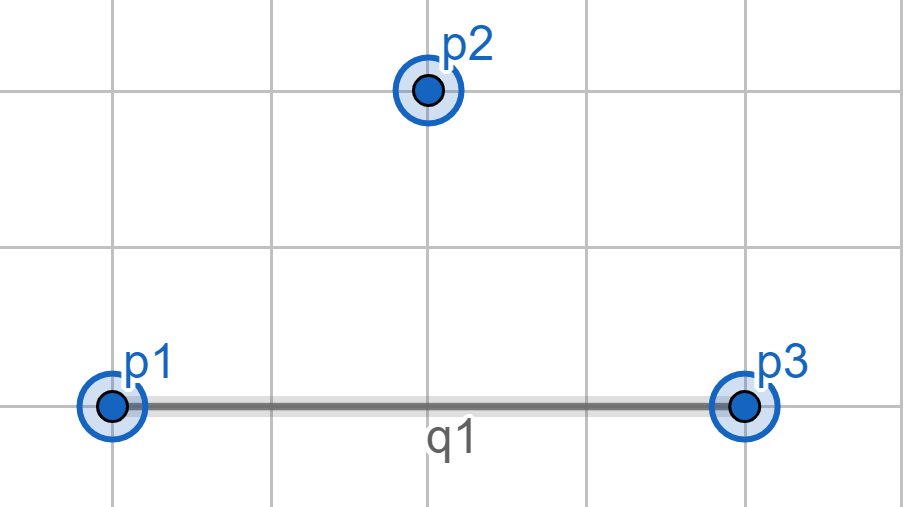
2: Is NOT a graph. q2 is part of the set Q, but it is not present in the graph.
3: Is NOT a graph. Graphs cannot be infinite.
4: Is a graph. Each vertex and edge in the graph is defined. This graph is finite and has no repititions.
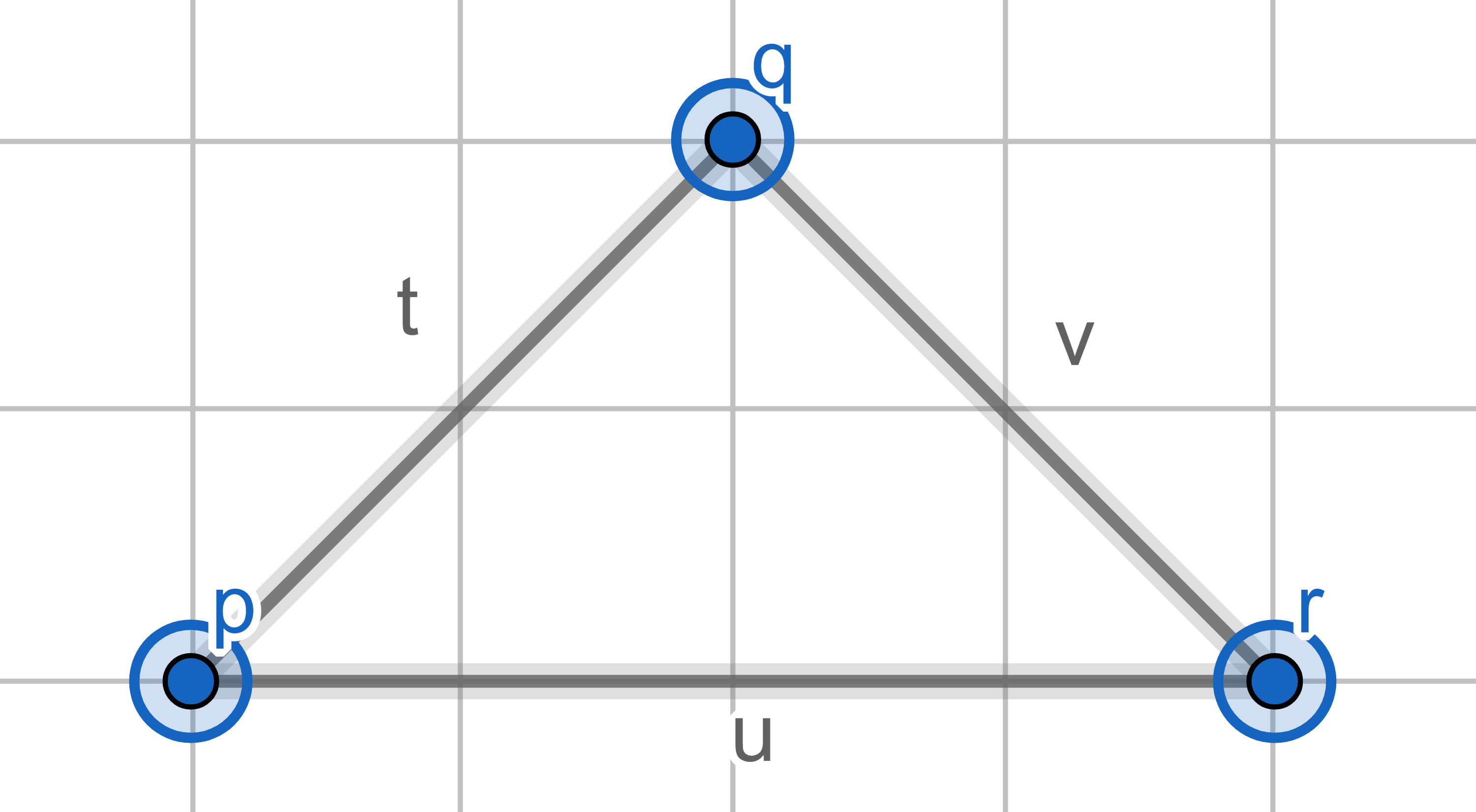
5: Is a graph. This graph is three unconnected points. We have seen in an example that a graph simply made of unconnected points is acceptable.
6: Is NOT a graph. u1u2 and u2u1 are the same edge. We cannot have a graph that has the same edge repeated.
7: Is NOT a graph. v3v3 is an edge that connects point v3 to itself. A point cannot be adjacent to itself.
8: Is a graph. Each vertex and edge in the graph is defined. This graph is finite and has no repititions.

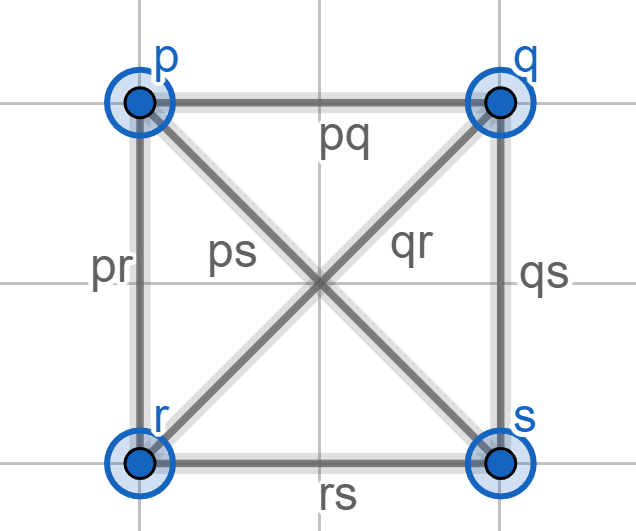
Definition 1.2.10.

Two vertices, \(v_i\) and \(v_j\text{,}\) in a graph \(G\) are adjacent if and only if \(v_iv_j\) is an edge in \(G\text{.}\)

Definition 1.2.11.

Two edges in a graph \(G\) are incident if and only if they share a vertex.

Problem 1.2.12.

In terms of the diagrams list properties required and properties not allowed in graphs.

Solution.

Must be finite
Two points cannot be connected by more than one edge to each other
Edges must connect to a distinct vertex at both ends of that edge
Vertex's and edges can be labeled
All Vertices do not need to be connected to each other

Problem 1.2.13.

In terms of the matrices list properties required and properties not allowed in graphs.

Problem 1.2.14.

In terms of the sets list properties required and properties not allowed in graphs.

Solution.

Allowed:

Empty set for edges
Can define a graph as a relation

Not allowed:

Empty set for vertices
Defining relations with undefined points
Defining a relation with itself (identity)
Infinite sets

Problem 1.2.15.

Match the properties that define a graph for each pair of notations.

Problem 1.2.16.

Write the matrix form of the first graph diagram in Figure 1.2.1.

Solution.

\(\left(\begin{array}{*{6}{r}} 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \end{array}\right)\)