Section 1.1 Motivation for Graph Theory
Problem 1.1.1. Friendship.
Guido is friends with Swen, Ute, Eva Marie, and Lars.
Swen is friends with Guido, Ute, Eva Marie, Lars, and Solveig.
Ute is friends with Guido, Swen, Eva Marie, and Solveig.
Eva Marie is friends with Guido, Swen, Ute, and Solveig.
Lars is friends with Guido, Swen, and Solveig.
Solveig is friends with Swen, Ute, Eva Marie, and Lars.
-
Represent the friendships above with a diagram.
By designating each person as a vertex and the friendships as edges, this diagram can be produced to represent who is friends with whom.
-
Find the largest clique, that is a group such that everyone knows everyone else. How did you find this group?
Beginning with the diagram in Figure 1.1.2, we can begin to find the largest clique by eliminating the node with the least connections. In this case, Lars.
Now that Lars is eliminated, we repeat the process until the only remaining people are all friends. In this case, we have two options. Solveig or Guido can be eliminated, each resulting in a clique of four friends.
-
If one of the people tells his or her friends a story, and each person who hears the story tells all of their friends, will the story reach everyone? How did you check this?
If one of the people tells his or her friends a story, and each person who hears the story tells all of their friends, will the story reach everyone? How did you check this?
Yes, this is because the graph is connected. And if any one person tells all their friends, Swen will hear it. And Swen is friends with everone



Problem 1.1.5. Toys.
Guido likes playing with planes, trains, and heavy equipment.
Eva Marie likes playing with trains, heavy equipment, and boats.
Swen likes playing with planes and boats.
Solveig likes playing with planes and trains.
-
Find a way that each person can play with one toy that they like.
Based on these statements, Table 1.1.6 shows which toys each person likes and dislikes. An "O" shows that the person likes a certain toy, and an "X" signifies dislike.
Since Swen only likes playing with planes and boats, I chose that Swen will play with planes. I can then mark that no one else can play with planes, and Swen can not play with any other toy. Notice that the only other person who likes playing with boats is Eva Marie, so she must play with that toy. Also notice that Solveig only likes planes and trains, and since the planes are taken, she must play with trains. This leaves Guido with heavy equipment. See Table 1.1.7
-
Find a different way if possible.
From the above statments, it is of no issue to construct a graph representing these relationships. Each vertex represents a person or a toy, and each edge represents a child liking that particular toy.
If we let Solveig play with planes, Swen with boats, Eva Marie with trains ad Guido with heavy equipment, then each child gets to play with one toy that they like. If we instead let Solveig play with planes, Swen with boats, Eva Marie with heavy equipment and Guido with trains, then each child still gets to play with a toy they like. Using the above graph, we can see clearly which children like which toys. If we start assigning toys to children, starting with the pickiest children (Swen and Solveig), we can give each child the opportunity to play with a toy they like. Making different choices at any point during the distribution will facilitate a different outcome.
How did you find the solutions?
| planes | trains | heavy equipment | boats | |
| Guido | O | O | O | X |
| Eva Marie | X | O | O | O |
| Swen | O | X | X | O |
| Solveig | O | O | X | X |
| planes | trains | heavy equipment | boats | |
| Guido | X | X | O | X |
| Eva Marie | X | X | X | O |
| Swen | O | X | X | X |
| Solveig | X | O | X | X |
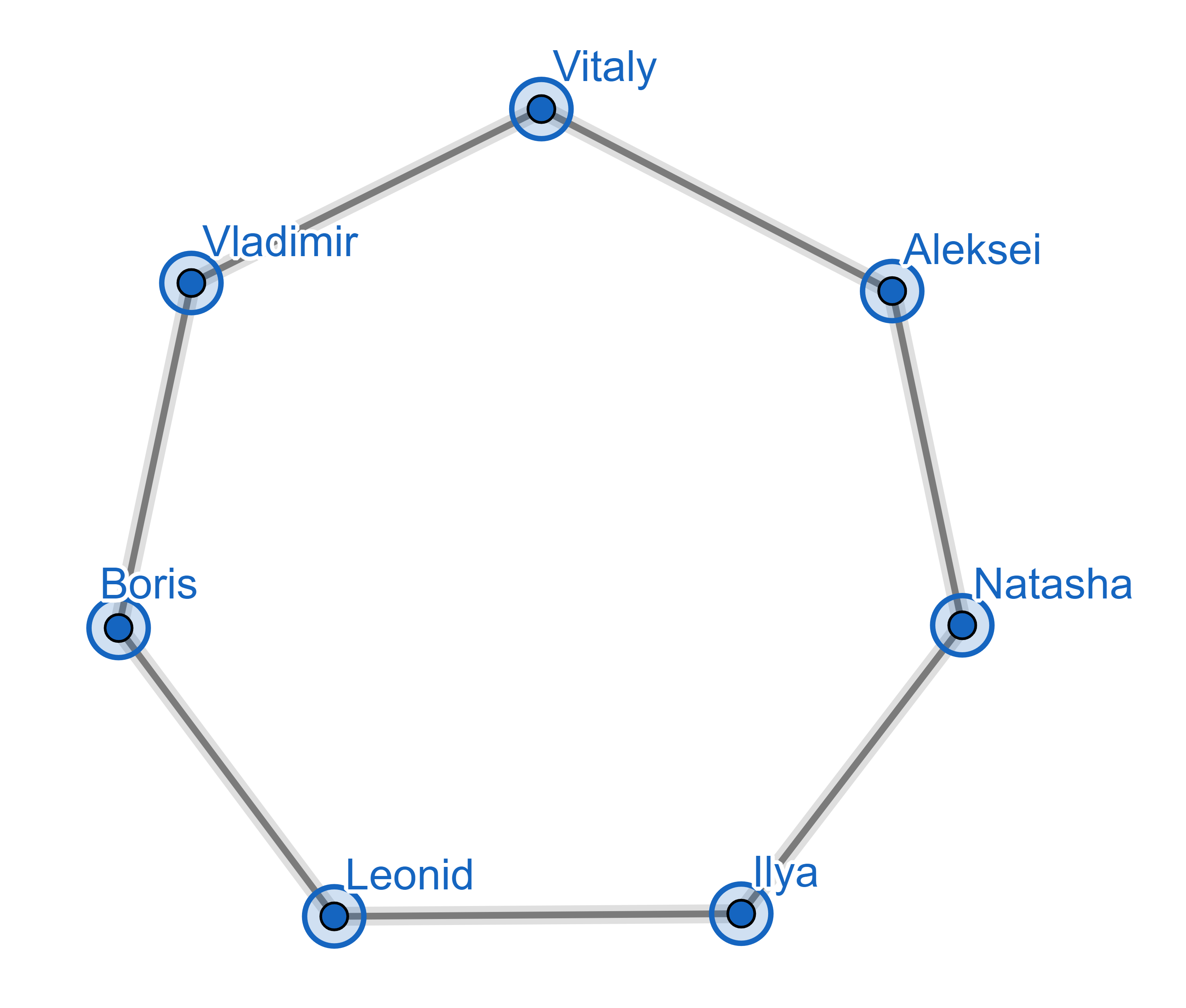
Problem 1.1.8. Effective Committees.
To ensure that work is accomplished a committee is established so that no two members are friends prior to the committee.
Boris knows Vladimir and Leonid.
Vitaliy knows Vladimir and Aleksei.
Natasha knows Aleksei and Dmitry.
Ilya knows Dmitry and Leonid.
Vladimir knows Boris and Vitaliy.
Aleksei knows Vitaliy and Natasha.
Dmitry knows Natasha and Ilya.
Leonid knows Ilya and Boris.
-
Find three people that meet the committee condition.
Aleksei, Leonid, Dmitry.
This group was found by slowly grouping people together one by one. Starting with Vitaliy then adding Leonid while making sure the pair match the committe condition. Dmitry is than added as the third person.
-
What is the largest group you can find that meets the committee condition?
The largest group is Boris, Vitaly, Natasha, Ilya. None of these individuals know each other.
To find 3 people who meet the conditions, simply find any 3 people who do not share an edge. See Figure 1.1.9. To find the largest group, chose every other person in the diagram to avoid choosing people who know each other (share an edge). This can be done 2 ways, and results in a group of 4 people.
How did you find these?
-
If Elena knows Aleksei and Dmitry, can you construct a larger committee?
Just to remind ourselves, let's take a look at the unaltered candidates one more time.
By adding Elena to the committee candidates, an interesting option appears. Since Elena knows both Aleksy and Dmitry, selecting her as a committee member eliminates all of the candidates that Natasha knows as well. This means that Natasha can be selected without eliminating any further members and a committee of five can be formed out of Elena, Natasha, Ilya, Boris, and Vitaly.
-
If Olga knows Vitaliy and Aleksei, can you construct a larger committee? (Ignore Elena).
Just to remind ourselves, let's take a look at the unaltered candidates one more time.
By adding Olga to the committee candidates, a circumstance is created in which three candidates all know each other. Any committee selection in which all candidates were exhauted would select a single member from this triumvirate, creating three cases:
Suppose Vitaly is selected. If so, then a committee of four members can be formed out of Vitaly, Boris, Ilya, and Natasha.
Suppose that Aleksy is selected. If so, then a committee of four members can be formed out of Aleksy, Dmitry, Leonid, and Vladimir.
Suppose that Olga is selected. If so, then two four-member committees are possible. One committee can be formed from Olga, Natasha, Ilya, and Boris. Another can be formed from Olga, Vladimir, Leonid, and Dmitry.
In all cases, the largest possible commitee is only four people. Thus, adding Olga does not increase or decrease the maximum committee size.
-
If Boris also knows Aleksei and Dmitry, Vitaliy also knows Dmitry and Leonid, Natasha also knows Vladimir and Leonid, and Ilya also knows Vladimir and Aleksei, does the size of the largest possible committee change? Explain. (Note ignore Elena and Olga for this problem).
No it does not change, Forming a group of 4 is still possible because each person is linked to someone 3 edges away, making it possible to choose committe members from the orifinal links - where everyone is two connections away.
Construct a diagram such that each of the original 8 employees is linked to everyone whom they do not know. Find the largest clique (group of directly linked people) in this structure.
Comment on this solution.
Problem 1.1.10. Advertising.
To maximize the benefit of “word of mouth” advertising, Trinkets Inc. wants to give out samples such that each person receives exactly one and no two friends have the same item.
Boris is friends with Elena, Aleksei, and Natasha.
Elena is friends with Aleksei and Boris.
Aleksei is friends with Boris, Elena, and Ilya.
Ilya is friends with Aleksei, Leonid, Vitaliy, and Natasha.
Leonid is friends with Ilya.
Vitaliy is friends with Ilya.
Natasha is friends with Ilya and Boris.
(a)
Find a way to use three different samples meeting the condition given.
Let the samples be named A, B, and C.
We'll start organizing who gets what sample with Ilya, Leonid, and Vitaliy.
Let Ilya have sample A.
Let Leonid have sample B.
Let Vitaliy have sample C.
Since Natasha is also friends with Ilya, she cannot have sample A, and since she is not friends with Leonid nor Vitaliy, we'll give her sample B.
Since Boris is friends with Natasha, he cannot have sample B, and since Boris is not friends with Ilya nor Vitaliy, we'll give him sample C.
This just leaves Elena and Aleksei
Since Elena is friends with Boris, she cannot have sample C. So she must have sample A or B.
Aleksei is friends with Boris, Elena, and Ilya. So being friends with Boris and Ilya, he cannot have samples A or C. Therefore he must have sample B.
Thus Elena must have sample A.
(b)
Can you find a way to use four different samples meeting the condition? If so, show it, if not explain why.
(c)
How many different types of samples could be used?
7 different types of samples could be used. If each individual receives a different type of sample, then no two friends have the same item.
(d)
Can you find a way to use only two different samples meeting the condition? If so, show it, if not explain why.














