Section 2.4 Graph Isomorphism
Problem 2.4.1.
Using the provided links to Geogebra, if possible re-arrange the vertices until the graphs in Geogebra look like the graphs below.



Definition 2.4.2. Graph isomorphism.
Two graphs \(G\) and \(G^\prime\) are isomorphic if and only if there exists a one-to-one and onto correspondence from the vertices of \(G\) to the vertices of \(G^\prime\) such that a pair of vertices in \(G\) is adjacent if and only if the corresponding pair of vertices in \(G^\prime\) are adjacent.








Definition 2.4.4. Clique.
A subgraph \(H\) of a graph \(G\) is a clique if an only if \(H\) is a complete graph.
Definition 2.4.5. Independent Set.
A subset of vertices \(H\) of a graph \(G\) is an independent set if an only if no two vertices in \(H\) are adjacent.
Problem 2.4.6.
For each of the graphs in Figure 2.4.3
count the number of vertices,
count the number of edges,
find the minimum degree (denoted \(\delta(G)\)),
find the maximum degree (denoted \(\Delta(G)\)),
find the the largest cycle,
find the the largest clique,
find the largest independent set.
-
Graph 1
V = 8
E = 16
\(\displaystyle \delta(G) = 4 = \Delta(G)\)
Largest cycle = 8
Largest clique = 2
Largest independent set = 4
-
Graph 2
V = 8
E = 16
\(\displaystyle \delta(G) = 4 = \Delta(G)\)
Largest cycle = 8
Largest clique = 3
Largest independent set = 2
-
Graph 3
V = 8
E = 16
\(\displaystyle \delta(G) = 4 = \Delta(G)\)
Largest cycle = 8
Largest clique = 3
Largest independent set = 2
-
Graph 4
V = 8
E = 12
\(\displaystyle \delta(G) = 3 = \Delta(G)\)
Largest cycle = 8
Largest clique = 2
Largest independent set = 4
-
Graph 5
V = 8
E = 16
\(\displaystyle \delta(G) = 4 = \Delta(G)\)
Largest cycle = 8
Largest clique = 2
Largest independent set = 4
-
Graph 6
V = 8
E = 12
\(\displaystyle \delta(G) = 3 = \Delta(G)\)
Largest cycle = 8
Largest clique = 2
Largest independent set = 4
-
Graph 7
V = 8
E = 16
\(\displaystyle \delta(G) = 4 = \Delta(G)\)
Largest cycle = 8
Largest clique = 2
Largest independent set = 4
-
Graph 8
V = 8
E = 12
\(\displaystyle \delta(G) = 3 = \Delta(G)\)
Largest cycle = 8
Largest clique = 2
Largest independent set = 4
Problem 2.4.7.
Find all sets of isomorphic graphs in the list above.
First we start by creating a graph, where ceach graph is represented by a node, and is only ajacent with another node if all the values calculated are the same.
Now we can see that graphs (2,3) and (5,7,1) and (4,6,8) are similer.
Problem 2.4.8.
Prove that each set of graphs above is isomorphic.
Let A map to I, B map to J, C map to L, D map to N, E map to p, F map to O, G map to M and H map to K. We can see then that the graphs would be identical, making graphs A and G isomorphic.

Let A map to I, B map to M, C map to N, D map to O, E map to K, F map to P, G map to L and H map to J. Similarly, let Let Q map to I, R map to M, Z map to N, V map to O, U map to K, T map to P, W map to L and S map to J. We can see then that the graphs would be identical, making graphs D, F and H isomorphic.

Let A map to I, B map to K, C map to J, D map to P, E map to L, F map to N, G map to O and H map to M. We can see then that the graphs would be identical, making graphs C and B isomorphic.

Problem 2.4.9.
Describe your personal algorithm for efficiently determining if two graphs are isomorphic.
Problem 2.4.10.
Draw and count the total number of connected, non-isomorphic graphs on 1,2,3, and 4 vertices.
1 Graph with 1 vertex, 1 Graph with 2 vertices, 2 graphs with 3 vertices, 6 graphs with 4 vertices
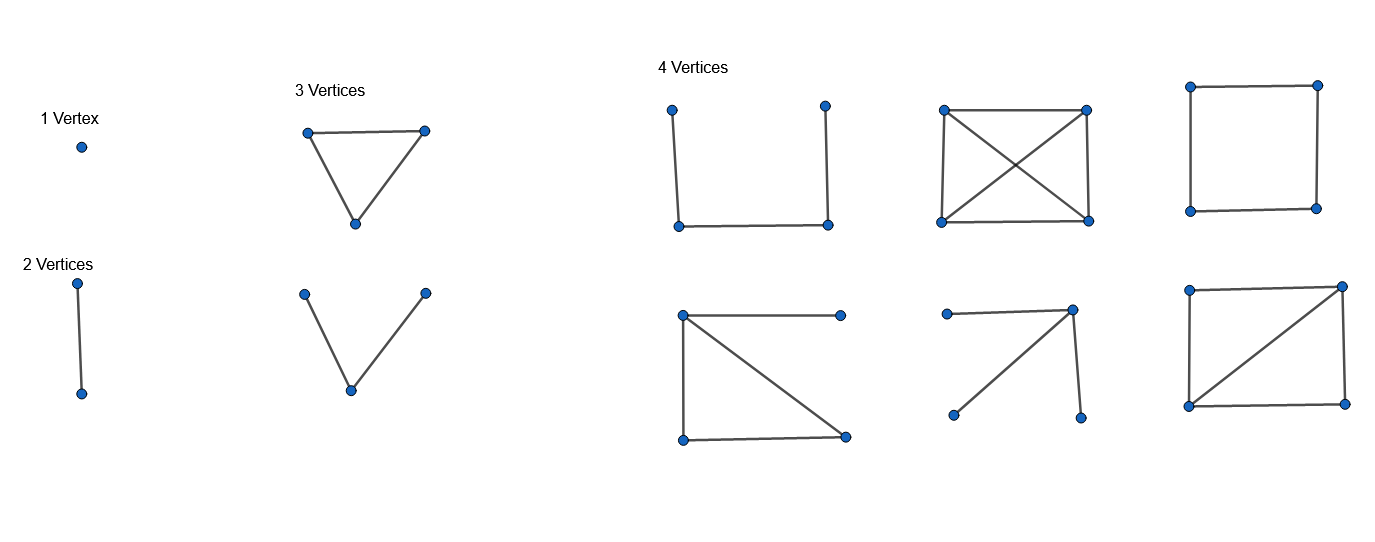
Problem 2.4.11.
Count the total number of non-isomorphic graphs on four vertices.
There is a total of 11 graphs

Problem 2.4.12.
Draw and count the total number of non-isomorphic trees on five vertices.
3 total non-isomorphic graphs



geogebra.org/classic/mypzu8xegeogebra.org/classic/chzvy39zgeogebra.org/classic/qadrmwnx